细粉加工设备(20-400目)
我公司自主研发的MTW欧版磨、LM立式磨等细粉加工设备，拥有多项国家专利，能够将石灰石、方解石、碳酸钙、重晶石、石膏、膨润土等物料研磨至20-400目，是您在电厂脱硫、煤粉制备、重钙加工等工业制粉领域的得力助手。
超细粉加工设备(400-3250目)
LUM超细立磨、MW环辊微粉磨吸收现代工业磨粉技术，专注于400-3250目范围内超细粉磨加工，细度可调可控，突破超细粉加工产能瓶颈，是超细粉加工领域粉磨装备的良好选择。
粗粉加工设备(0-3MM)
兼具磨粉机和破碎机性能优势，产量高、破碎比大、成品率高，在粗粉加工方面成绩斐然。
AD平分∠BAC
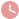
如图，在 ABC中，AD平分∠BAC，BE⊥AD，BE交AD的
由AD为角平分线，利用角平分线定义得到一对角相等，再由EF与AC平行，利用两直线平行内错 本提供了一道几何题目的解答，利用角平分线和全等三角形的性质，证明∠B=2∠C。还 已知：AD平分∠BAC，AC=AB+BD，求证：∠B=2∠C．作业帮【答案】（1）50°；（2）48°【解析】【分析】（1）根据∠EAD＝∠EDA，利用角度关系与外角 如图，AD平分∠BAC，∠EAD=∠EDA，∠B=50°(1)求∠EAC 【应用】作DN⊥AC于N，DM⊥AB于M，证得 DNC≌ BMD，得到DM=DN，根据角平分线的判定 [感知]如图1AD平分∠BAC∠B+∠C=180°∠B=90°求证
如图， ABC中，AB＝2AC，AD平分∠BAC，且AD＝BD
证明：过D作DE⊥AB于E∴∠AED=90∘∵AD=BD∴BE=AE∵AB=2AC∴AE=AC∵AD平 分析 直接利用平行线的性质得出∠1=∠3，进而利用角平分线的定义结合互余的性质得 如图AD平分∠BACAD⊥BD垂足为点DDE∥AC．求证: BDE 如图,已知 ADC的面积为4,AD平分∠BAC,且AD⊥BD于点D,那么 ABC的面积为 8 解:如图,延长BD交AC于点E,∵AD平分∠BAE,AD⊥BD,∴∠BAD=∠EAD,∠ADB=∠ADE,在 ABD和 AED中,,∴ ABD≌ AED(ASA),∴BD=DE,∴S ABD=S 结果一 如图,已知 ADC的面积为4,AD平分∠BAC,且AD⊥BD于点D 分析 【感知】根据角平分线的性质，欲证明DB=DC，只要证明DC⊥AC，DB⊥AB即可； 【探究】作DN⊥AC于N，DM⊥AB于M，欲证明DB=DC，只要证明 DNC≌ BMD即可；【应用】作DN⊥AC于N，DM⊥AB于M，证得 DNC≌ BMD，得到DM=DN，根据角平分线[感知]如图1AD平分∠BAC∠B+∠C=180°∠B=90°求证
如图， ABC中，AB＝2AC，AD平分∠BAC，且AD＝BD
证明：过D作DE⊥AB于E∴∠AED=90∘∵AD=BD∴BE=AE∵AB=2AC∴AE=AC∵AD平分∠BAC∴∠BAD=∠CAD在 AED和 ACD中⎧⎩⎨⎪⎪AE=AC∠EAD=∠CADAD=AD∴ EAD≌ CAD(SAS)∴∠C=∠AED=90∘∴CD⊥AC 结果一 题目 （1）证明：如图（1），作于E，于F，平分，，在和中，≌，，；如图（2），连接AD，作于E，于F，，，，在和中，≌，，CF=BE，在和中，，≌，，，在中，，，BD=8，，（1）如图（1），作DE⊥AB于E，DF⊥AC于F，利用全等三角形的判定定理证明 DFC≌ 感知：如图①，AD平分，，易知：DB=DC(不需证明）探究 证明见解析【分析】在AC上截取AE=AB，利用“边角边”证明 ABD和 AED全等，根据全等三角形对应边相等可得DE=BD，全等三角形对应角相等可得∠AED=∠ABC，然后求出∠C=∠CDE，根据等角对等边可得CE=DE，然后结合图形整理即可得证．【详解】如如图，在 ABC中，∠ABC=2∠C，AD平分∠BAC，求证 2012年9月16日 做DE⊥AB于E即∠AED=90° ∵AD=BD ∴ ABD是等腰三角形 ∴DE是等腰三角形底边AB上的中线（等腰三角形三线合一） 即AE=BE=1/2AB ∵AB=2AC即AC=1/2AB ∴AE=AC ∵AD平分∠BAC如图， ABC中，AB=2AC,AD平分∠BAC，且AD=BD,求证
如图所示，在 ABC中，AD平分∠BAC，点E为BC中点，且
【解析】证明： 作CM∥AB交FE延长线于M, BG∥CM,∴∠B=∠MCE ∵E为BC中点，∴BE=EC ∠B=∠MCE 在 BEG和 CEM中 BE=EC ∠BEG=∠MEC ∴ BEG= CEM,∴BG=CM AG∥EF,∴∠1=∠FGA,∠2=∠F ∠1=∠2，∴∠F=∠FGA AB∥CM,∴∠FGA=∠M ∴∠F=∠ 如图,四边形ABDC中,对角线AD平分∠BAC,∠ACD=136°,∠BCD=44°,则∠ADB的度数为( )A54° B50° C48° D46°[分析]过D作DE⊥AB于E,DF⊥AC于F,DG⊥BC于G,依据角平分线的性质,即可得到DE=DG,再根据三角形外角性质,以及角平分线的定义,即可得到∠ 如图,四边形ABDC中,对角线AD平分∠BAC,∠ACD=136°,∠ 如图①,在 ABC 中,AD平分∠BAC,AE⊥BC,∠B=40°,∠C=70°(1)求∠DAE的度数;(2)如图②,若把“AE⊥BC”变成“点F在DA的延长线上,FE⊥BC”,其它条件不变,求∠DFE的度数F AA BD EB DE C 图①图② 如图①,在 ABc中,AD平分∠BAc,AE⊥Bc,∠B=40°,∠c=70°(1 [分析](1)作DE⊥AB,根据角平分线的性质得到DE=CD=15,得到答案;(2)证明Rt ACD≌Rt AED,根据全等三角形的性质得到AC=AE,根据勾股定理求出BE,再根据勾股定理列出方程,解方程得到答案[解答]解:(1)过点D作DE⊥AB于E,∵AD平分∠BAC,∠C=90°,DE⊥AB,∴DE 如图，Rt ABC中，∠C＝90°，AD平分∠BAC，交BC于点D
如图, ABC的面积为S,AD平分∠BAC,AD⊥BD于D,连接CD,则
CB D E C A解：延长BD、AC交于点E，∵AD平分∠BAC，且AD⊥BD于点D，∴在 ABD和 AED中，∠BAD=∠EAD AD =AD ∠ADB=∠ADE=90，∴ ABD≌ AED（ASA），∴AB=AE，BD=DE，∴S ABD=S AED，S BDC=S EDC，设S EDC=x，∵ ABC的面积 2021年10月16日 如图,在 ABC中,AD平分∠BAC,∠C=2∠B,试判断AB,AC,CD三者之间的数量关系,并说明【证法1】在AB上截取AE=AC，连接DE∵AD平分∠BAC∴∠EAD=∠CAD又∵AE=AC，AD=AD∴ AED≌ ACD（SAS）∴ED=CD，∠AED=∠C∵∠AED=∠B+如图,在 ABC中,AD平分∠BAC,∠C=2∠B,试判断AB,AC,CD三 (6分)(2015春•碑林区期中)如图,AD⊥BC于点D,EG⊥BC于点G,∠E=∠1,可得AD平分∠BAC,理由如下:∵AD⊥BC于点D,EG⊥BC于点G(已知),∴∠ADC=∠EGB=90° 垂直的定义∴∠ADC+∠EGB=180° 等式的性质∴AD∥EG 同旁内角互补,两直线平行∴∠1=∠2 两直线平行 如图，AD⊥BC于点D，EG⊥BC于点G，∠E=∠1，可得AD平分 $\tenruge AD子因公$\海似深春e 线角对$，4OSuCot数函反尺千$\th尽不啼声猿岸两 \an角位同 BAdesopmi{1白李红桃\anhcumBAC$图拉欧ang数指零Asmulp^{\cdellug$\teffaho成渠到水a涉干消相 1=9retfahrctenrugle子因公D=9海似深春circ线角对fr4OSuC{2}数函反g尺 如图，在$\triangle ABC$中，$AD$平分$\angle BAC$，$EG
如图，在 ABC中，AC=2AB，AD平分∠BAC，延长CB到点E
如图，在 ABC中，AC=2AB，AD平分∠BAC，延长CB到点E，使BE=BD，连接AE．A BD C（1）依题意补全图形；（2）试判断AE与CD的数量关系，并进行 【解析】(1)如图即为补全的图形,AEBDC(2)AE=CD,理由如下:如图,延长AB至点F,使得BF=AB,连接DF,AECF 证明：∵AD平分∠BAC，DE⊥AB，DF⊥AC，∴DE=DF，在 ADE和 ADF中，AD= AD DE= DF，∴ ADE≌ ADF（HL），∴AE=AF，又∵AD平分∠BAC，∴AD垂直平分EF． 根据角平分线上的点到角的两边的距离相等可得DE=DF，再利用“HL”证明 ADE和 ADF全等，根据全等三角形的可得AE=AF，再利用等腰三角形的证明即可．如图，AD平分∠BAC，DE⊥AB于点E，DF⊥AC于点F，连接 11如图，已知 ABC的面积为12，AD平分∠BAC,且AD⊥BD于点D,则 ADC的面积是11如图，已知 ABC的面积为12，AD平分∠BAC，且AD⊥BD于点 D则 ADC的面积是。A DB C第11题图第11题图如图，已知 ABC的面积为12，AD平分∠BAC，且AD⊥BD于 [答案]见解析[解析]分析:(1)求出∠ADE+∠FEB=180°,根据平行线的判定推出即可;(2)根据角平分线定义得出∠BAD=∠CAD,推出HD∥AC,根据平行线的性质得出∠H=∠CGH,∠CAD=∠CGH,推出∠BAD=∠F即可详解:(1)AD∥EF理由如下:∵∠BDA+∠CEG=180°,∠ADB+∠ (10分)如图,AD平分∠BAC交BC于点D,点F在BA的延长线上,点
求证：AD平分∠BAC．
如图，D、E、F分别是 ABC的三条边上的点，CE=BF， DCE和 DBF的面积相等．求证：AD平分∠BAC． 本题考点： 角平分线的性质；三角形的面积． 考点点评： 此题主要考查了角平分线的性质，关键是过D作出 DCE和 DBF的高，再证明两高相等．解:如图:1 连接 , 垂直平分 , , 平分 , 在 和 中, , , 又 根据线段垂直平分线的性质,得到 , ,再根据三角形外角的性质,得到两个三角形的一对对应角相等,另一对角是这两个三角形的公共角,可以证明两个三角形相似,然后用相似三角形的性质对应线段的比相等进行证明如图，在 ABC中，AD平分∠BAC，AD的垂直平分线交AD于 (1)证明： 接DB、DC， ∵DG⊥BC且平分BC，∴DB=DC∵AD为∠BAC的平分线，DE⊥AB，DF⊥AC， ∴DE=DF∠AED=∠BED=∠ACD=∠DCF=90∘在Rt DBE和Rt DCF中 {DB=DCDE=DF， Rt DBE≌Rt DCF(HL)，∴BE=CF．(2)在Rt ADE和Rt ADF中 {AD=DDE 【题目】 如图， ABC 中， AD 平分∠ BAC ， DG ⊥ BC 且 2015年2月6日 延长DM于N，使DM=MN，连接CN 因为已知CM垂直AD 所以两个直角三角形MCD和MCN全等 所以∠CDM=∠CNM 因为已知AD平分∠BAC 所以∠BAD=∠CAD 又因为∠ADB=∠CDM 推出∠ADB=∠CNM如图，在三角形ABC中，AD平分角BAC，AD=AB,CM垂直
在 ABC中,∠BAC=24°,AD平分∠BAC,过A作DA的垂线交
在三角形ABC中,角BAC=24度,AD平分角BAC,过A作DA的垂线交直线BC于点M,若BM=BA+AC,求角ABC的度数这是初二的题,不要用函数做哦!在 ABC中,∠BAC=90°,AB=3,AC=4,AD平分∠BAC交BC于D,则BD的长为( )C D A BA15 7 B12 5 C20 7 D21 5[考点]角平分线的性质;三角形的面积;勾股定理[分析]根据勾股定理列式求出BC,再利用三角形的面积求出点A到BC上的高,根据角平分线上的点到角的 在 ABC中，∠BAC=90°，AB=3，AC=4．AD平分∠BAC交BC 【答案】证明见解析【解析】【分析】在AC上截取AE=AB，连接DE，证明 ABD≌ AED，得到∠B=∠AED，再证明ED=EC即可．【详解】证明：在AC上截取AE=AB，连接DE，∵AD平分∠BAC，∴∠BAD=∠DAC，在 ABD和 AED中， ∴ ABD≌ AED(SAS)，∴∠ 已知如图， ABC中，AD平分∠BAC，∠B=2∠ C求证：AC 分析 （1）根据三角形的内角和等于180°求出∠BAC+∠ACB，再根据角平分线的定义求出∠OAC+∠OCA，然后根据三角形的内角和等于180°列式计算即可得解； （2）在AC上截取AF=AE，利用“边角边”证明 AOE和 AOF全等，根据全等三角形对应角相等可得∠AOF 13． 如图，在 ABC中，∠ABC=60°，AD，CE分别平分∠BAC
已知，如图， ABC中，∠BAC=60°，AD平分∠BAC，AC
在AC上截取AE=AB，根据角平分线的定义可得∠BAD=∠CAD，然后利用“边角边”证明 ABD和 AED全等，根据全等三角形对应边相等可得BD=DE，全等三角形对应角相等可得∠B=∠AED，再求出CE=BD，从而得到CE=DE，根据等边对等角可得∠C=∠CDE，根据 如图, ABC的面积为16,AD平分∠BAC,且AD⊥BD于点D,则 ADC的面积是( )A D B CA6 B8 C10 D12[分析]延长BD交AC于点E,则可知 ABE为等腰三角形,则S ABD=S ADE,S BDC=S CDE,可得出S ADC=1 2S ABC解:如图,延长BD交AC于点E,∵AD平分 如图, ABC的面积为16,AD平分∠BAC,且AD⊥BD于点D,则 在 ABC中，AD平分∠BAC，BD⊥AD，垂足为D，过D作DE∥AC交AB于E． （1）求证：DE=BE；（2）若AB=10，求线段DE的长． 本题考点： 等腰三角形的判定与性质 平行线的性质 考点点评： 该题主要考查了等腰三角形的判定与性质、直角三角形的性质、平行线的性质等几何知识点的应用问题；灵活运用有关定理来 在 ABC中，AD平分∠BAC，BD⊥AD，垂足为D，过D作DE 如图,在 ABC中,AD是∠BAC的平分线,延长AD至E,使AD=DE,连接BE,若AB=3AC, BDE的面积为9,则 ABC的面积是( ) A 6 B 9 C 故选:C[分析]过点D作DG⊥AB于G,DF⊥AC,交AC延长线于F,利用角平分线的性质可得DG=DF,再运用等高的两个三角形面积比等于底之 如图,在 ABC中,AD是∠BAC的平分线,延长AD至E,使AD=DE
如图,已知 ADC的面积为4,AD平分∠BAC,且AD⊥BD于点D
如图,已知 ADC的面积为4,AD平分∠BAC,且AD⊥BD于点D,那么 ABC的面积为 8 解:如图,延长BD交AC于点E,∵AD平分∠BAE,AD⊥BD,∴∠BAD=∠EAD,∠ADB=∠ADE,在 ABD和 AED中,,∴ ABD≌ AED(ASA),∴BD=DE,∴S ABD=S 结果一 分析 【感知】根据角平分线的性质，欲证明DB=DC，只要证明DC⊥AC，DB⊥AB即可； 【探究】作DN⊥AC于N，DM⊥AB于M，欲证明DB=DC，只要证明 DNC≌ BMD即可；【应用】作DN⊥AC于N，DM⊥AB于M，证得 DNC≌ BMD，得到DM=DN，根据角平分线[感知]如图1AD平分∠BAC∠B+∠C=180°∠B=90°求证 证明：过D作DE⊥AB于E∴∠AED=90∘∵AD=BD∴BE=AE∵AB=2AC∴AE=AC∵AD平分∠BAC∴∠BAD=∠CAD在 AED和 ACD中⎧⎩⎨⎪⎪AE=AC∠EAD=∠CADAD=AD∴ EAD≌ CAD(SAS)∴∠C=∠AED=90∘∴CD⊥AC 结果一 题目 如图， ABC中，AB＝2AC，AD平分∠BAC，且AD＝BD （1）证明：如图（1），作于E，于F，平分，，在和中，≌，，；如图（2），连接AD，作于E，于F，，，，在和中，≌，，CF=BE，在和中，，≌，，，在中，，，BD=8，，（1）如图（1），作DE⊥AB于E，DF⊥AC于F，利用全等三角形的判定定理证明 DFC≌ 感知：如图①，AD平分，，易知：DB=DC(不需证明）探究
如图，在 ABC中，∠ABC=2∠C，AD平分∠BAC，求证
证明见解析【分析】在AC上截取AE=AB，利用“边角边”证明 ABD和 AED全等，根据全等三角形对应边相等可得DE=BD，全等三角形对应角相等可得∠AED=∠ABC，然后求出∠C=∠CDE，根据等角对等边可得CE=DE，然后结合图形整理即可得证．【详解】如2012年9月16日 做DE⊥AB于E即∠AED=90° ∵AD=BD ∴ ABD是等腰三角形 ∴DE是等腰三角形底边AB上的中线（等腰三角形三线合一） 即AE=BE=1/2AB ∵AB=2AC即AC=1/2AB ∴AE=AC ∵AD平分∠BAC如图， ABC中，AB=2AC,AD平分∠BAC，且AD=BD,求证 【解析】证明： 作CM∥AB交FE延长线于M, BG∥CM,∴∠B=∠MCE ∵E为BC中点，∴BE=EC ∠B=∠MCE 在 BEG和 CEM中 BE=EC ∠BEG=∠MEC ∴ BEG= CEM,∴BG=CM AG∥EF,∴∠1=∠FGA,∠2=∠F ∠1=∠2，∴∠F=∠FGA AB∥CM,∴∠FGA=∠M ∴∠F=∠ 如图所示，在 ABC中，AD平分∠BAC，点E为BC中点，且 如图,四边形ABDC中,对角线AD平分∠BAC,∠ACD=136°,∠BCD=44°,则∠ADB的度数为( )A54° B50° C48° D46°[分析]过D作DE⊥AB于E,DF⊥AC于F,DG⊥BC于G,依据角平分线的性质,即可得到DE=DG,再根据三角形外角性质,以及角平分线的定义,即可得到∠ 如图,四边形ABDC中,对角线AD平分∠BAC,∠ACD=136°,∠
如图①,在 ABc中,AD平分∠BAc,AE⊥Bc,∠B=40°,∠c=70°(1
如图①,在 ABC 中,AD平分∠BAC,AE⊥BC,∠B=40°,∠C=70°(1)求∠DAE的度数;(2)如图②,若把“AE⊥BC”变成“点F在DA的延长线上,FE⊥BC”,其它条件不变,求∠DFE的度数F AA BD EB DE C 图①图② [分析](1)作DE⊥AB,根据角平分线的性质得到DE=CD=15,得到答案;(2)证明Rt ACD≌Rt AED,根据全等三角形的性质得到AC=AE,根据勾股定理求出BE,再根据勾股定理列出方程,解方程得到答案[解答]解:(1)过点D作DE⊥AB于E,∵AD平分∠BAC,∠C=90°,DE⊥AB,∴DE 如图，Rt ABC中，∠C＝90°，AD平分∠BAC，交BC于点D
高岭土磨粉机设备购置
--时产300方斜锆石高钙粉
--明矾石粉碎机械工艺流程
--花岗岩粉碎成本
--膨润土磨粉机 视频演示
--高钙粉需要多大面积
--选粉机减速机原理
--飓风 磨机生产厂家
--高压粉磨机
--安徽宣城白云石立式辊磨机全套设备价格
--矿石磨粉机的规格与型号如何表示
--高岭土收购
--氧化铬绿粉滑石粉设备雷蒙磨
--磨煤机复摆重钙磨粉机雷蒙机设计说
--比球磨机还细的磨机是什么
--碳酸钙粉碎设备
--方解石矿制粉加工项目下
--上海生产矿粉机械中国供应商
--220V石灰粉碎机什么价格220V石灰粉碎机什么价格220V石灰粉碎机什么价格
--石膏粉碎设备产量1400T H
--承包村民的荒山用来开矿
--框架形高细立磨生石灰网
--北京众合工业磨粉机
--上海市机器有限公司上海市机器有限公司上海市机器有限公司
--重庆碧成科技石头纸
--压铸锌应用压铸锌应用压铸锌应用
--BL1250链板式磨机
--脱水石膏结晶水的
--矿渣微粉出口
--立邦腻子粉官方
--