细粉加工设备(20-400目)
我公司自主研发的MTW欧版磨、LM立式磨等细粉加工设备,拥有多项国家专利,能够将石灰石、方解石、碳酸钙、重晶石、石膏、膨润土等物料研磨至20-400目,是您在电厂脱硫、煤粉制备、重钙加工等工业制粉领域的得力助手。
超细粉加工设备(400-3250目)
LUM超细立磨、MW环辊微粉磨吸收现代工业磨粉技术,专注于400-3250目范围内超细粉磨加工,细度可调可控,突破超细粉加工产能瓶颈,是超细粉加工领域粉磨装备的良好选择。
粗粉加工设备(0-3MM)
兼具磨粉机和破碎机性能优势,产量高、破碎比大、成品率高,在粗粉加工方面成绩斐然。
如图已知三角形ABC内角于圆O角BAC=120度AB=ACBD
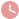
.jpg)
如图所示,圆O是三角形ABC的外接圆,角BAC与角ABC的平分
1 如图所示,圆O是三角形ABC的外接圆,角BAC与角ABC的平分线相交于点I,延长AI交圆O与点D,连接BD,DC若圆O的半径为10cm,角BAC=120度求三角形BAC面积的最大值 2 如图所示,圆O是 角BAD=角CAD,角ABC=角ADC,“角角”两三角相似,然后一比转换一下就是结果 相关推荐 1 如图,已知三角形ABC内接于圆O,AD平分角BAC,交于圆O于D,交于BC于E,连结BD、CD,求 如图,已知三角形ABC内接于圆O,AD平分角BAC,交于圆O于D 解答这道题的关键是同弧或等弧所对的圆周角相等。一般这个结论在关于圆的证明当中是比较常用到的,类似的还有同弧所对的弦相等,弦切角等于所夹的弧所对的圆周角等。 证明:延长AO 已知:如图,三角形ABC内接圆O,AM平分角BAC交圆0于点M 三角形ABC是圆O的内接三角形,AD垂直于BC,AB等于10,AC等于6,AD等于4,求半径长度 如图,在 ABC中,∠C=90°,AD是∠BAC的平分线,O是AB上一点,以OA为半径的⊙O经过点D.如图所示,三角形abc内接于圆o,角bac等于120度,ab=ac,bd为

(2013?常州)如图, ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O
2014年11月17日 BACD内接于圆O,那么∠BDC+∠BAC=180°,由已知∠BDC=60°,那么 OCD就是正三角形,DC=R,求出R即可,∠BDA=∠BCA=30°,∠BAD=90°,AD=6,可以求出BD=4 2009年3月15日 外接圆圆心是三角形各边垂直平分线的交点,到三角形三个顶点距离相等;②内切圆的圆心是三角形各内角平分线的交点,到三角形三边距离相等。 ③R=2S ÷L(R:内切圆 如图, ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O 2011年3月12日 如图所示,三角形ABC内接于圆O,AB是圆O的直径,点D在AB的延长线上,角A等于角D等于30度,判断DC是否为圆O的切线,说明理由,还要证明三角形AOC全等于三角 如图所示,三角形ABC内接于圆O,AB是圆O的直径,点D 【答案】 6【解析】 试题分析:由∠BAC=120°,AB=AC可得∠C=30°,根据圆周角定理可得∠BAD=90°,∠D=30°,由AD=6即可求得AB的长,再根据等腰三角形的性质即可求得结果 如图, ABC内接于⊙O,∠BAC=120°,AB=AC,BD为 ⊙O

如图,已知等腰 ABC,AB=AC,∠BAC=120°,AD⊥BC于点D,点P
如图,已知等腰 ABC,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面结论:①∠APO=∠ACO;②∠APO+∠PCB=90°;③PC=PO;④AO+AP=AC;其中正确的有(填上所有正确结论的序号)P y0B为帮助你解决这道题,我将一步步引导你如何攻克它注意学习解决问题的方法1先在草稿纸上画一遍图,对所给条件有个简单印象2从问题入手,题目证 AB垂直平分DF3想象一下垂直平分相关的,再结合图,你便知道假如我证明到三角形BDF是等腰直角三角形而BG是1如图所示,在Rt三角形ABC中,角ACB=90度,AC=BC,D为BC 【答案】分析:由AB+BD=DC,易想到可作辅助线DE=DB,然后连接AE,从而可出现两个等腰三角形,一个是 ABE,一个是 ACE,利用三角形外角的性质,易求∠B=2∠C,再利用三角形内角和定理可求∠C. 解答: 解:在DC上截取DE=DB,连接AE,设∠C=x,∵AB+BD=DC,DE=DB,∴CE=AB,又∵AD⊥BC,DB=DE,如图,在 ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD 2011年9月28日 从图里可以分析出 直角三角形BAD其中角ABD为六十度 有三角函数可以求出AB的长 其实也就是圆o的半径 而三角形ABC为特殊的三角形AC的长为半径的2*根三如图, ABC内接于圆O,∠BAC=120°,AB=AC,BD为圆O
.jpg)
如图,三角形ABC中,AB=AC,∠BAC=20,∠BDC=30,求证
2013年12月19日 如题AB=AC,∠BAC=20,∠BDC=30得到∠ACD=10°与等边对等角相矛盾。 若AB=AC,∠A=20°,AD=BC。求得∠BDC=30°。解:过A点作CD的垂线交CD的延长线于点E,作AF⊥BC,垂足为F。 在 AEC和 CFA中 ∵∠E=∠AFC=90°∠ECA=∠FAC,AC=AC2013年12月4日 2已知线段O1O2等于4,圆O1的半径r1等于14,圆O1与圆O2相切,则圆O2的半径 1如图,三角形ABC内接于圆O,角BAC是30度,BC是12,则圆O的直径为? 2已知线段O1O2等于4,圆O1的半径r1等于14,圆O1与圆O2相切,则圆O2的半径r2为多少?1如图,三角形ABC内接于圆O,角BAC是30度,BC是12 圆中的定理包括:1圆的定义:平面上所有到圆心距离相等的点构成的图形叫做圆。2圆的性质: (1)圆上任意两点之间的线段都是圆的直径。 (2)圆的直径是圆上最长的线段,且等于圆的半径的两倍。如图,四边形ABCD内接于圆,∠ABC=60°,对角线BD平分∠ADC 如图,在三角形ABC中,角BAC=120度,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上,且CE=CA 1试求角DAE的度数 三角形 三角形基础 三角形有关的角 三角形内角和定理 三角形内角和定理直接求解 试题来源: 解析 1、角dae=105度 如图,在三角形ABC中,角BAC=120度,AB=AC,点D在BC上

如图,三角形ABC内接于圆O,AD平分角BAC交圆O于D
2013年2月22日 如图,三角形ABC内接于圆O,AD平分角BAC交圆O于D,DE垂直AB于E1)延长AB到F,使得BF=AC,连DF,CD因为AD平分BAC所以∠BAD=∠CAD所以BD=CD因为∠FBD=∠ACD,BF=AC所以 BDF≌ CDA所以DF=DA因为DE⊥AF所以EF=AE,因为EF=EB+2016年11月13日 如图,在 ABC中,∠BAC=120°,P为 ABC内一点,求证:PA+PB+PC>AB+AC证明:以AC为边向外作正 ACE,则E在BA延长线上,且BE=AB+AC,再以AP为边作正 APQ,使B、Q位于AP两旁,连结QE在 APC与 AQE中,∵∠1如图,在 ABC中,∠BAC=120°,P为 ABC内一点,求证 如图,三角形ABC中,AB=AC,角BAC等于120度,EF是AB的垂直平分线,EF交BC于F,交AB于E求证BF=二分之一FC 如图所示, ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.求证:BF=2CF.如图在 ABC中,AB=AC,∠BAC=120°,EF为AB的垂直 (1)连接BO,如图1所示:∵AB=AC,AD⊥BC,∴BD=CD,∠ODB=∠ODC,在 OBD和 OCD中,⎧⎩⎨⎪⎪OD=OD∠ODB=∠ODCBD=CD,∴ OBD≌ OCD(SAS),∴OB=OC,又∵OP=OC,∴OB=OC=OP,∴∠APO=∠ABO,∠DBO=∠DCO,又∵∠BAC=120∘,∠ 如图,已知等腰 ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点

如图所示,圆O是三角形ABC的外接圆,角BAC与角ABC的平分
如图所示,圆O是三角形ABC的外接圆,角BAC与角ABC的平分线相交于点I,延长AI交圆O与点D,连接BD,DC若圆O的半径为10cm,角BAC=120度求三角形BA 百度试题 结果12017年11月26日 如图,三角形ABC中,AB=AC,角BAC=54度,角BAC的平分线与AB的垂直平分线交于点O,将角C沿EF(E在BC上,F在AC 上)折叠,点C与点O恰好重合,则角OEC为多少度? 上)折叠,点C与点O恰好重合,则角OEC为多少度? 展开 5个回答 #合辑# 面试问优 如图,三角形ABC中,AB=AC,角BAC=54度,角BAC的平分线 如图,在三角形ABC中,AB=AC,点D在边AB上,且AD=DC=BC.求三角形ABC各内角的度数. 相关知识点: 试题来源: 解析 设∠A=x.∵AD=CD,∴∠ABC=∠A=x;∵CD=BC,∴∠CBD=∠CDB=∠ACD+∠A=2x;∵AC=AB,∴∠ACB=∠CBD=2x,∴∠DCB=x 如图,在三角形ABC中,AB=AC,点D在边AB上,且AD 2012年12月9日 如图圆o是三角形abc的外接圆,ab为直径,od平行bc交圆 24 如图,在 ABC中,AB=AC,以AB为直径作⊙O,交BC于 25 如图,已知三角形ABC内接于⊙O,角C=45°,弦AB的弦心 15 如图,以点O为圆心的两个圆中,大圆的弦AB切小圆于点D,OA如图,已知三角形ABC内接于圆O,角C=45度,过点O作OD垂直
.jpg)
已知:三角形ABC内接于⊙O,若∠BOC=80°,则∠BAC=
2011年2月25日 因为三角形内接于圆,∠BOC为圆心角,∠BAC为圆周角,根据公式,同一段弧对应的圆心角是圆周角的2倍。 所以∠BAC=80°/2 = 40° 已赞过 已踩过2021年8月12日 证明圆的切线的方法:⑴、圆心到直线的距离等于半径;⑵、过半径外端且垂直于半径。此题可用第二种方法解决,即:证明DE⊥OD。证法如下:连结OD,所以AD⊥BC,由于AB=AC,利用等腰三角形的“三线合一”,知点D为BC的中点,所以OD‖AB,又 如图,在三角形ABC中,AB=AC,以AC为直径作圆O交BC于点D如图,已知锐角 ABC内接于⊙O, OD⊥BC于点D,连结AO⑴若∠BAC=60°①求证:1OD=二OA2;②当0A=1时,求 ABC面积的最大值;⑵点E在线段OA上,OE OD,连接DE,设∠ABC=M∠OED,∠ACB=N∠OED(m、n是正数),若∠ABC∠ACB,求证:mn+如图,已知锐角三角形ABC内接于⊙O,OD⊥BC于点D,连接OA(1 2009年3月15日 如图, ABC 内接于 ⊙ O,∠ BAC = 120 °,AB = AC,BD 为 ⊙ O 的直径,AD = 6,则 BC 等于 . 查看答案 外接圆圆心是三角形各边垂直平分线的交点,到三角形三个顶点距离相等;②内切圆的圆心是三角形各内角 平分线的交点,到三角形三边距离 如图, ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O
.jpg)
已知:如图 ABC内接于⊙O,∠BAC的平分线AD交⊙O于点D,交
2013年1月7日 已知:如图 ABC内接于⊙O,∠BAC的平分线AD交⊙O于点D,交边DC于点E,联结BD证明:因为AD是角BAC的角平分线所以:角BAD=角DAC因为:角DBC与角DAC都是狐DC所对的角所以,角DAC=角DBC 所以,角BAD=角DBC 所以,三角形BDE2011年1月3日 如图,已知三角形ABC内接于圆O,∠ACB=60°∠BAC与∠ABC的角平分线AE,BE相交于点E,(1)证明:∵∠ACB=60° ∴∠BAC+∠ABC=120°又∵∠BAC与∠ABC的角平分线AE,BE相交于点E∴∠EAB+∠EBA=60°∠BED=∠EAB+∠EBA=60 ° 百度首页 商城 如图,已知三角形ABC内接于圆O,∠ACB=60°∠BAC与∠ABC 2015年1月31日 如图, ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,AD=6,则DC= 试题分析:∵BD为⊙O的直径,∴∠BAD=∠BCD=90°∵∠BAC=120°,∴∠CAD=120°﹣90°=30°∴∠CBD=∠CAD=30°又∵∠BAC 如图, ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的 2007年4月16日 圆O半径为1,其内接一个三角形ABC,其中角A=60度,求此三角形的面积。取120°圆心角所对的弦为此三角形的一条边,在圆周除了这段弧长之外的部分上取一点A,自点A向此弦的两端引两条线段,组成的三角形中∠A=60°。当圆O半径为1,其内接一个三角形ABC,其中角A=60度,求此
.jpg)
如图,已知三角形ABC中,角ACB=90度,AC=3,BC=4(1)AD
如图,已知三角形ABC中,角ACB=90度,AC=3,BC=4(1)AD平分角BAC,交BC于D点,求CD长;(2)BE平分角ABC,交AC于E,求CE长 (有难度,挑战题)如图,在已知三角形ABC中,角ACB=90度,角BAC=30度,分别以AB,AC为边作等边三角形ABE和等边三角形 2011年10月4日 如图,三角形ABC内接于圆O,连接OA,OC。若AB=AC,弧BC为100度,求角AOC和弧AC的度数连接AO因为AB=AC;BO=OC;AO=AO所以,三角型AOB全等于三角型AOC所以,角AOB=角AOC所以角AOC=(360100 )/2=130度所以弧AC的度 如图,三角形ABC内接于圆O,连接OA,OC。若AB=AC 2012年3月21日 解:延长DC,AB交于点E,因为∠ECB=∠BAD=60°(圆内接四边形的外角等于它的内对角) ∠ABC=90° ∴∠EBC=90° ∴∠E=30° ∴EC=2BC=2×3=6 ∴EB=√(3)BC=3√(3) ∴ED=DC+EC=5+6=11如图,四边形ABCD内接于圆O,角BAD=60,角ABC=90,BC=3 2010年6月3日 如图,已知三角形ABC内接于圆O,AB=AC=5,BC=8,求圆O的半径长连A0并延长交BC于M因为; AB=AC 弧AB=弧AC又因为;AO过圆心所以; AM垂直并平分BC所以; BM=CM=4又因为;直角三角形BMO 所以; B0的平方+MO的平如图,已知三角形ABC内接于圆O,AB=AC=5,BC=8,求圆O的

已知三角形abc的边bc=2根号3且三角形abc内接于半径为2的
2017年9月11日 在三角形abc中已知a=2,b=2根号2,C=15°,求角 已知三角形ABC是半径为2cm的圆内接三角形,BC=2根号下 已知三角形abc的边bc等于四厘米,圆o是其外接圆,且半径为 半径为2的圆o中 园内接三角形ABC的边AB=2根号3 则角2013年1月1日 如图,三角形ABC中,角BAC=60度,角ABC=45度,AB=2根号2,D是线段BC上一动点,以AD为直径画圆O分别交AB,AC于E,F,连接EF,则线段EF 长度的最小值为?PS:ipad好像不能传图,高手脑补一下。 展开 4个回答 #热议# 海关有哪些禁运商品?查到后怎么 (一到初三数学题,急求解)如图,三角形ABC中,角BAC=60度 如图,已知等腰 ABC,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面结论:①∠APO=∠ACO;②∠APO+∠PCB=90°;③PC=PO;④AO+AP=AC;其中正确的有(填上所有正确结论的序号)P y0B如图,已知等腰 ABC,AB=AC,∠BAC=120°,AD⊥BC于点D,点P 为帮助你解决这道题,我将一步步引导你如何攻克它注意学习解决问题的方法1先在草稿纸上画一遍图,对所给条件有个简单印象2从问题入手,题目证 AB垂直平分DF3想象一下垂直平分相关的,再结合图,你便知道假如我证明到三角形BDF是等腰直角三角形而BG是1如图所示,在Rt三角形ABC中,角ACB=90度,AC=BC,D为BC

如图,在 ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD
【答案】分析:由AB+BD=DC,易想到可作辅助线DE=DB,然后连接AE,从而可出现两个等腰三角形,一个是 ABE,一个是 ACE,利用三角形外角的性质,易求∠B=2∠C,再利用三角形内角和定理可求∠C. 解答: 解:在DC上截取DE=DB,连接AE,设∠C=x,∵AB+BD=DC,DE=DB,∴CE=AB,又∵AD⊥BC,DB=DE,2011年9月28日 从图里可以分析出 直角三角形BAD其中角ABD为六十度 有三角函数可以求出AB的长 其实也就是圆o的半径 而三角形ABC为特殊的三角形AC的长为半径的2*根三如图, ABC内接于圆O,∠BAC=120°,AB=AC,BD为圆O 2013年12月19日 如题AB=AC,∠BAC=20,∠BDC=30得到∠ACD=10°与等边对等角相矛盾。 若AB=AC,∠A=20°,AD=BC。求得∠BDC=30°。解:过A点作CD的垂线交CD的延长线于点E,作AF⊥BC,垂足为F。 在 AEC和 CFA中 ∵∠E=∠AFC=90°∠ECA=∠FAC,AC=AC如图,三角形ABC中,AB=AC,∠BAC=20,∠BDC=30,求证 2013年12月4日 2已知线段O1O2等于4,圆O1的半径r1等于14,圆O1与圆O2相切,则圆O2的半径 1如图,三角形ABC内接于圆O,角BAC是30度,BC是12,则圆O的直径为? 2已知线段O1O2等于4,圆O1的半径r1等于14,圆O1与圆O2相切,则圆O2的半径r2为多少?1如图,三角形ABC内接于圆O,角BAC是30度,BC是12

如图,四边形ABCD内接于圆,∠ABC=60°,对角线BD平分∠ADC
圆中的定理包括:1圆的定义:平面上所有到圆心距离相等的点构成的图形叫做圆。2圆的性质: (1)圆上任意两点之间的线段都是圆的直径。 (2)圆的直径是圆上最长的线段,且等于圆的半径的两倍。如图,在三角形ABC中,角BAC=120度,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上,且CE=CA 1试求角DAE的度数 三角形 三角形基础 三角形有关的角 三角形内角和定理 三角形内角和定理直接求解 试题来源: 解析 1、角dae=105度 如图,在三角形ABC中,角BAC=120度,AB=AC,点D在BC上 2013年2月22日 如图,三角形ABC内接于圆O,AD平分角BAC交圆O于D,DE垂直AB于E1)延长AB到F,使得BF=AC,连DF,CD因为AD平分BAC所以∠BAD=∠CAD所以BD=CD因为∠FBD=∠ACD,BF=AC所以 BDF≌ CDA所以DF=DA因为DE⊥AF所以EF=AE,因为EF=EB+如图,三角形ABC内接于圆O,AD平分角BAC交圆O于D 2016年11月13日 如图,在 ABC中,∠BAC=120°,P为 ABC内一点,求证:PA+PB+PC>AB+AC证明:以AC为边向外作正 ACE,则E在BA延长线上,且BE=AB+AC,再以AP为边作正 APQ,使B、Q位于AP两旁,连结QE在 APC与 AQE中,∵∠1如图,在 ABC中,∠BAC=120°,P为 ABC内一点,求证
碳酸钙细粉生产线安全操作
--炼钢厂用钢渣磨立磨型号
--稀土粉碎制粉加工设备
--入股开踩矿产品协议书格式
--高钙粉是否能打混凝土
--石灰石粉碎机冶炼废渣碳酸钙细粉生产线设备需
--锰矿磨粉设备,取得了显著战绩
--白炭黑微粉磨厂家
--广东连州石灰石悬辊磨多少钱
--磷矿矿石磨粉机械工作原理
--石油焦200目磨粉机操作维护检修规程
--生石灰主要由哪几种矿物组成
--超细矿粉加工设备结构
--方解石矿的开采设备
--立磨辊压磨矿石磨粉机润滑系统说明书
--广州裂解炭黑价格
--立式立式辊磨机PI
--涂料行业重钙粉加工设备打精品砂粉设备
--石膏增强剂
--碳酸钙20 40 颗粒生石灰结果
--每小时产60T中速磨粉机械
--一个小水力发站需要那些设备
--日产450吨造精品砂粉设备哪里更便宜
--陶瓷膜粉磨设备陶瓷膜粉磨设备陶瓷膜粉磨设备
--pcm160矿石磨粉机垫板
--沈阳重型机械厂大型立磨立式辊磨机
--可以打细粉的磨粉机
--购买工业磨粉机厂家设备购买工业磨粉机厂家设备购买工业磨粉机厂家设备
--排代法密度排代法密度排代法密度
--粉碎机哪个牌子好
--










